9matric/o JED
9matrico
- 1.
 Reliefa modelo:
bulo, peco aŭ muldilo, per kiu oni povas
fabriki similajn pecojn per fandado, frapo, giso, premo:
monerojn oni frapas per matrico.
Reliefa modelo:
bulo, peco aŭ muldilo, per kiu oni povas
fabriki similajn pecojn per fandado, frapo, giso, premo:
monerojn oni frapas per matrico.
- a)
 Formo por gisi litertipojn.
Formo por gisi litertipojn.
- b)
-
Kartona formo preme reproduktita de kompostaĵo, per kiu oni
povas gisi
stereotipon1.
 kliŝo1
kliŝo1 - c)
- (en galvanoplastiko)
Formo, kiu kovriĝas per maldika tavolo de metalo.
 patrico
patrico
- 2.

 Kliŝo2:
iu el la produktantoj ŝatas akiri pli
da profito kaj kaŝe ofertas al kopiemuloj la matricon de la
filmo
[1];
aperis duvoluma Katalogo […],
kies (hektografajn)
matricojn, por 554 paĝoj,
Steiner skribis mem
[2].
Kliŝo2:
iu el la produktantoj ŝatas akiri pli
da profito kaj kaŝe ofertas al kopiemuloj la matricon de la
filmo
[1];
aperis duvoluma Katalogo […],
kies (hektografajn)
matricojn, por 554 paĝoj,
Steiner skribis mem
[2].
- 3.
 Grundomaso, de rokoj, konsistanta el grajnetaj kristaloj,
ĉirkaŭanta pli grandajn kristalojn:
en Sudafriko, diamantoj ofte estas ekstraktataj el matrico de
argila roko (kimberlito) nomita „flava grundo“
[3].
Grundomaso, de rokoj, konsistanta el grajnetaj kristaloj,
ĉirkaŭanta pli grandajn kristalojn:
en Sudafriko, diamantoj ofte estas ekstraktataj el matrico de
argila roko (kimberlito) nomita „flava grundo“
[3].
- 4.
 PIV1
(kun `n` horizontaloj kaj
p vertikaloj):
en lineara algebro, determinanto estas funkcio kiu asociigas
skalaron `det(A)` al ĉiu
`n xx n` kvadrata matrico
[4];
memadjunkta matrico aŭ hermita matrico estas kvadrata matrico
kun kompleksaj
elementoj kiu estas egala al sia konjugita transpono
[5].
PIV1
(kun `n` horizontaloj kaj
p vertikaloj):
en lineara algebro, determinanto estas funkcio kiu asociigas
skalaron `det(A)` al ĉiu
`n xx n` kvadrata matrico
[4];
memadjunkta matrico aŭ hermita matrico estas kvadrata matrico
kun kompleksaj
elementoj kiu estas egala al sia konjugita transpono
[5].
 (n,p)-matrico
(n,p)-matrico- 5.
 Dudimensia tabelo:
tiun analizon oni povas prezenti per la matrico (6), en kiu la simbolo + indikas
pozitivan valoron de la koncerna trajto binara, la simbolo – negativan
(malan) valoron
[6];
usonaj filmoj kiel „La matrico“ aŭ „Okuloj larĝe fermitaj“
levas la demandon pri la svagaj limoj inter realo kaj sonĝo,
inter efektivo kaj imago, inter frenezo kaj racio
[7].
Dudimensia tabelo:
tiun analizon oni povas prezenti per la matrico (6), en kiu la simbolo + indikas
pozitivan valoron de la koncerna trajto binara, la simbolo – negativan
(malan) valoron
[6];
usonaj filmoj kiel „La matrico“ aŭ „Okuloj larĝe fermitaj“
levas la demandon pri la svagaj limoj inter realo kaj sonĝo,
inter efektivo kaj imago, inter frenezo kaj racio
[7].
 vektoro
vektoro
Rim.:
Ne konfuzu kun:
utero (latine: matrix).
1.
Monato, Fidilalao Henriel: Kontraŭleĝa
kopiado
2. Ivo Lapenna, Tazio Carlevaro kaj Ulrich Lins: Esperanto en Perspektivo, Kvara Parto
3. Vikipedio, Matrico mineralogia
4. Vikipedio, Determinanto
5. Vikipedio, Memadjunkta matrico
6. John Christopher Wells: Lingvistikaj aspektoj de Esperanto, 2. Fonetiko
7. Jorge Camacho: Pri realo kaj la malo, Monato, 2000/09, p. 23
2. Ivo Lapenna, Tazio Carlevaro kaj Ulrich Lins: Esperanto en Perspektivo, Kvara Parto
3. Vikipedio, Matrico mineralogia
4. Vikipedio, Determinanto
5. Vikipedio, Memadjunkta matrico
6. John Christopher Wells: Lingvistikaj aspektoj de Esperanto, 2. Fonetiko
7. Jorge Camacho: Pri realo kaj la malo, Monato, 2000/09, p. 23
- angle:
- matrix 4. matrix
- beloruse:
- матрыца
- ĉine:
- 模 [mú], 模具 [mújù], 模型 [móxíng], 模子 [múzi], 矩阵 [jǔzhèn], 矩陣 [jǔzhèn], 方阵 [fāngzhèn], 方陣 [fāngzhèn]
- france:
- 4. matrice
- germane:
- 1. Matrize 2. Negativ (Film) 3. Matrix 4. Matrix 5. Tabelle
- hispane:
- matriz
- hungare:
- mátrix 1.a anyaminta 1.b matrica 1.c anyaforma 1. matrica (alakítószerszám) 4. mátrix
- japane:
- 鋳型 [いがた], 金型 [かながた], 抜き型 [ぬきがた], 母型 [ぼけい], 行列 [ぎょうれつ], 石基 [せっき], 基質 [きしつ]
- nederlande:
- 1.c matrijs 1. matrijs 4. matrix 5. matrix
- pole:
- 4. macierz
- portugale:
- 1.c matriz 1. matriz 4. matriz 5. matriz
- ruse:
- матрица 4. матрица
- ukraine:
- матриця, материнська порода, жильна порода
matrici
(tr)
- Formi per matrico: li transdonis al sinjoro Povondra vizitkarton, sur kiu estis matricita ankro [8].
8.
Karel Čapek, trad. J. Vondroušek: Milito kontraŭ salamandroj, libro 1a, ĉapitro
3a
- angle:
- form a matrix
- beloruse:
- утвараць матрыцу
- france:
- matricer
- germane:
- eine Matrix bilden, eine Matrix formen
- hispane:
- formar una matriz
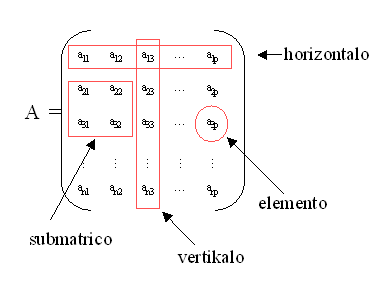
(n,p)-matrico
 (super komuteca
korpo `bb K`)
Bildigo de
`bb I xx bb J` al
`bb K`, kie
`bb I={1,2,...,n}`
kaj
`bb J={1,2,...,p}`:
matricon `A` oni kutime signas kiel
familion, t.e.
per skribaĵo `(a_(ij))_(i,j in bb I xx bb J)`,
kie `a_(ij)` signas
la bildon de
`(i,j)` per `A` kaj estas nomata
elemento (aŭ koeficiento) de `A`
kun indico `(i,j)`;
la nombrojn da horizontaloj kaj vertikaloj de
`(n,p)`-matrico oni nomas
ties dimensioj kaj signas ilin per skribaĵo de la tipo
`(n,p)` aŭ
`n xx p`;
eblas prezenti al si `(n,p)`-matricon
`A` kiel rektangulan tabelon, ĉe la interkruciĝo
de kies `i`-a horizontalo kaj
`j`-a
vertikalo staras la elemento
`a_(ij)`.
Rim.: Multaj fakaj terminoj rilatantaj al matricoj baziĝas sur la ĉi-supre menciita tabela metaforo.
(super komuteca
korpo `bb K`)
Bildigo de
`bb I xx bb J` al
`bb K`, kie
`bb I={1,2,...,n}`
kaj
`bb J={1,2,...,p}`:
matricon `A` oni kutime signas kiel
familion, t.e.
per skribaĵo `(a_(ij))_(i,j in bb I xx bb J)`,
kie `a_(ij)` signas
la bildon de
`(i,j)` per `A` kaj estas nomata
elemento (aŭ koeficiento) de `A`
kun indico `(i,j)`;
la nombrojn da horizontaloj kaj vertikaloj de
`(n,p)`-matrico oni nomas
ties dimensioj kaj signas ilin per skribaĵo de la tipo
`(n,p)` aŭ
`n xx p`;
eblas prezenti al si `(n,p)`-matricon
`A` kiel rektangulan tabelon, ĉe la interkruciĝo
de kies `i`-a horizontalo kaj
`j`-a
vertikalo staras la elemento
`a_(ij)`.
Rim.: Multaj fakaj terminoj rilatantaj al matricoj baziĝas sur la ĉi-supre menciita tabela metaforo. Malpli fakece:
matrico kun n horizontaloj
kaj p vertikaloj;
Malpli fakece:
matrico kun n horizontaloj
kaj p vertikaloj;
 Partoj de matrico:
horizontalo,
vertikalo,
diagonalo,
submatrico;
elemento,
indico de elemento,
koeficiento,
termo;
atributoj de matrico:
dimensioj,
ajgeno,
rango,
spuro,
determinanto,
minoro,
kofaktoro;
rimarkindaj ecoj de matrico:
kvadrata,
diagonala,
diagonaligebla,
triangula,
simetria,
hermita,
regula;
operacioj super matricoj:
matrica adicio,
matrica multipliko,
multipliko de matrico
per skalaro,
transpono;
Partoj de matrico:
horizontalo,
vertikalo,
diagonalo,
submatrico;
elemento,
indico de elemento,
koeficiento,
termo;
atributoj de matrico:
dimensioj,
ajgeno,
rango,
spuro,
determinanto,
minoro,
kofaktoro;
rimarkindaj ecoj de matrico:
kvadrata,
diagonala,
diagonaligebla,
triangula,
simetria,
hermita,
regula;
operacioj super matricoj:
matrica adicio,
matrica multipliko,
multipliko de matrico
per skalaro,
transpono;
 Specifaj matricoj:
unuomatrico,
nulmatrico,
matrico de homomorfio,
jakobia matrico de bildigo,
horizontalo,
vertikalo.
Specifaj matricoj:
unuomatrico,
nulmatrico,
matrico de homomorfio,
jakobia matrico de bildigo,
horizontalo,
vertikalo.
- angle:
- n-by-p matrix
- beloruse:
- матрыца памерам n×p
- france:
- matrice n×p
- germane:
- (n,p)-Matrix
- hungare:
- n×p méretű mátrix
- pole:
- macierz n×p
- ruse:
- матрица размера n×p
nulmatricoMatVort , matrica nulo
 (n,p)-Matrico,
kies
ĉiuj elementoj estas nulaj:
nulmatrico estas nulo rilate al
la
matrica adicio.
(n,p)-Matrico,
kies
ĉiuj elementoj estas nulaj:
nulmatrico estas nulo rilate al
la
matrica adicio.
- angle:
- null matrix
- beloruse:
- нуль-матрыца
- ĉine:
- 零矩阵 [língjǔzhèn], 零矩陣 [língjǔzhèn]
- france:
- matrice nulle
- germane:
- Nullmatrix
- hungare:
- nullmátrix
- pole:
- macierz zerowa
- ruse:
- нуль-матрица
submatrico
 (de (n,p)-matrico
`A`)
Tia `(n′,p′)`-matrico
`B`, ke
(1) `n′ le n` kaj
`p′ le p`,
(2) la elemento de `B` kun indico
`(i,j)` egalas al la elemento de
`A`
kun indico `(alpha(i),beta(j))`,
kie `alpha` (respektive `beta`)
estas strikte
kreskanta bildigo
de `{1,2,...,n′}`
al `{1,2,...,n}`
(respektive de `{1,2,...,p′}`
al `{1,2,...,p}`):
el `(n,p)`-matrico oni povas
formi
`p` submatricojn kun dimensioj
`(n,1)`;
eblas prezenti al si submatricon `B` per tio,
kio
restas
el matrico `A`, kiam oni forstrekis iujn
horizontalojn
kaj vertikalojn de ĝi.
(de (n,p)-matrico
`A`)
Tia `(n′,p′)`-matrico
`B`, ke
(1) `n′ le n` kaj
`p′ le p`,
(2) la elemento de `B` kun indico
`(i,j)` egalas al la elemento de
`A`
kun indico `(alpha(i),beta(j))`,
kie `alpha` (respektive `beta`)
estas strikte
kreskanta bildigo
de `{1,2,...,n′}`
al `{1,2,...,n}`
(respektive de `{1,2,...,p′}`
al `{1,2,...,p}`):
el `(n,p)`-matrico oni povas
formi
`p` submatricojn kun dimensioj
`(n,1)`;
eblas prezenti al si submatricon `B` per tio,
kio
restas
el matrico `A`, kiam oni forstrekis iujn
horizontalojn
kaj vertikalojn de ĝi.
- angle:
- submatrix
- beloruse:
- падматрыца
- ĉeĥe:
- submatice
- france:
- sous-matrice
- germane:
- Untermatrix
- hungare:
- részmátrix
- pole:
- podmacierz
- ruse:
- подматрица
- slovake:
- submatica
unuomatrico, matrica unuo
 (n,p)-Matrico,
kies
ĉiuj termoj estas nulaj, krom la diagonalaj, kiuj egalas al la
unuo:
la unuomatricon oni kutime signas per `I`;
unuomatrico estas unuo rilate al
la matrica multipliko.
(n,p)-Matrico,
kies
ĉiuj termoj estas nulaj, krom la diagonalaj, kiuj egalas al la
unuo:
la unuomatricon oni kutime signas per `I`;
unuomatrico estas unuo rilate al
la matrica multipliko.
- angle:
- unit matrix
- beloruse:
- матрыца адзінкавая
- ĉine:
- 单位矩阵 [dānwèijǔzhèn], 單位矩陣 [dānwèijǔzhèn]
- france:
- matrice unité
- germane:
- Einheitsmatrix
- hungare:
- egyésgmátrix
- pole:
- macierz jednostkowa
- ruse:
- единичная матрица
jakobia matrico
 (de bildigo
`f`
de `p`-dimensia al `n`-dimensia
normohavaj spacoj,
diferencialebla ĉe punkto
`a`)
La (n,p)-matrico
de ĝia diferencialo
ĉe `a`:
la ĝenerala elemento de la jakobia matrico de
`f` ĉe `a` egalas
al
`del_jf_i(a)`.
(de bildigo
`f`
de `p`-dimensia al `n`-dimensia
normohavaj spacoj,
diferencialebla ĉe punkto
`a`)
La (n,p)-matrico
de ĝia diferencialo
ĉe `a`:
la ĝenerala elemento de la jakobia matrico de
`f` ĉe `a` egalas
al
`del_jf_i(a)`.
 Jakobio,
jakobiano.
Jakobio,
jakobiano.
- angle:
- Jacobian matrix
- beloruse:
- матрыца Якобі
- ĉine:
- 雅可比矩阵 [yǎkěbǐjǔzhèn], 雅可比矩陣 [yǎkěbǐjǔzhèn]
- france:
- matrice jacobienne
- germane:
- Jacobische Matrix
- hungare:
- Jacobi-mátrix
- pole:
- macierz Jacobiego, macierz jakobianowa
- ruse:
- функциональная матрица
matrico de vektora homomorfio
 (p.p. homomorfio
`f`
de
`p`-dimensia vektora
spaco
`bb E` al `n`-dimensia
`bb F`,
ambaŭ super korpo `bb K`, rilate al
respektivaj
bazoj
`bb B_(bb E)`
kaj `bb B_(bb F)`)
Tia (n,p)-matrico `A`
super `bb K`, ke
`a_(ij)`
estas la `i`-a
komponanto
laŭ bazo `bb B_(bb F)`
de la bildo per `f` de la `j`-a
vektoro
de `bb B_(bb E)`:
la matrico de endomorfio estas kvadrata;
la matrico de idento estas
la unuomatrico;
la matrico de kunligaĵo de du homomorfioj egalas al la produto
de la matricoj de ĉiu homomorfio.
(p.p. homomorfio
`f`
de
`p`-dimensia vektora
spaco
`bb E` al `n`-dimensia
`bb F`,
ambaŭ super korpo `bb K`, rilate al
respektivaj
bazoj
`bb B_(bb E)`
kaj `bb B_(bb F)`)
Tia (n,p)-matrico `A`
super `bb K`, ke
`a_(ij)`
estas la `i`-a
komponanto
laŭ bazo `bb B_(bb F)`
de la bildo per `f` de la `j`-a
vektoro
de `bb B_(bb E)`:
la matrico de endomorfio estas kvadrata;
la matrico de idento estas
la unuomatrico;
la matrico de kunligaĵo de du homomorfioj egalas al la produto
de la matricoj de ĉiu homomorfio.
- angle:
- matrix of a linear mapping
- beloruse:
- матрыца лінейнага пераўтварэньня
- france:
- matrice d'application linéaire
- germane:
- Matrix einer linearer Abbildung
- hungare:
- vektor-homomorfizmus mátrixa
- pole:
- macierz odwzorowania liniowego
- ruse:
- матрица линейного преобразования
administraj notoj
pri
unuo~o, ~a unuo:
(n,p)-~o: Mankas fonto, kiu estas nek vortaro nek terminaro.
nul~o, ~a nulo: Mankas fonto, kiu estas nek vortaro nek terminaro.
sub~o: Mankas dua fontindiko.
sub~o: Mankas fonto, kiu estas nek vortaro nek terminaro.
unuo~o, ~a unuo: Mankas dua fontindiko.
unuo~o, ~a unuo: Mankas fonto, kiu estas nek vortaro nek terminaro.
jakobia ~o: Mankas dua fontindiko.
jakobia ~o: Mankas fonto, kiu estas nek vortaro nek terminaro.
~o de vektora homomorfio: Mankas dua fontindiko.
~o de vektora homomorfio: Mankas fonto, kiu estas nek vortaro nek terminaro.
Mi ne trovis aŭtoritatan fonton por tiu termino. MatVort
havas "~a unito" kaj "~unito", kiun mi opinias duoble
nekonvenaj: unue pro la uzo de "unito" kaj due pro la ordo
de elementoj. Mi preferis terminon paralelan al "nulmatrico",
"nulvektoro". [MB]
(n,p)-~o:
Mankas dua fontindiko.
(n,p)-~o: Mankas fonto, kiu estas nek vortaro nek terminaro.
nul~o, ~a nulo: Mankas fonto, kiu estas nek vortaro nek terminaro.
sub~o: Mankas dua fontindiko.
sub~o: Mankas fonto, kiu estas nek vortaro nek terminaro.
unuo~o, ~a unuo: Mankas dua fontindiko.
unuo~o, ~a unuo: Mankas fonto, kiu estas nek vortaro nek terminaro.
jakobia ~o: Mankas dua fontindiko.
jakobia ~o: Mankas fonto, kiu estas nek vortaro nek terminaro.
~o de vektora homomorfio: Mankas dua fontindiko.
~o de vektora homomorfio: Mankas fonto, kiu estas nek vortaro nek terminaro.